Skip to contents

denim DSL

Source: vignettes/denim_dsl.Rmd
denim_dsl.Rmd

Model definition in denim

In denim, model is defined by a set of transitions between compartments. Each transition is provided in the form of a key-value pair, where:

  • key show the transition direction between 2 compartments.

  • value is an expression that describe the transition, it can be a math expression or a built-in dwell-time distribution function.

These key-value pairs can be provided in 2 ways

  • Using denim domain-specific language (DSL).

  • Define as a list in R.

Denim DSL

In denim, each line of code must be a transition. The syntax for defining a transition in denim DSL is as followed:

compartment_A -> compartment_B = transition

Model definition written in denim DSL must be parsed by the function denim_dsl()

Math expression

For math expression, some basic supported operators include: + for addition, - for minus, * for multiplication, / for division, ^ for power. Users can also define additional model parameters in the math expression.

Math expressions in denim are parsed using muparser. For a full list of operators, visit the muparser website at https://beltoforion.de/en/muparser/features.php.

Distribution functions

Several built-in functions are provided to describe transitions based on the distribution of dwell time:

Each of these functions accepts either fixed numerical values or model parameters as inputs for their distributional parameters.

Define a classic SIR model

A classic SIR model can be defined in denim as followed

sir_model <- denim_dsl({
  S -> I = beta * (I/N) * S
  I -> R = d_exponential(rate = gamma)
})

denim_dsl() parses the given expression and return an R list as followed.

sir_model
#> $`S -> I`
#> [1] "beta * (I/N) * S"
#> 
#> $`I -> R`
#> Discretized exponential distribution
#> Rate = gamma
#> 
#> attr(,"class")
#> [1] "denim_transition"

In this example, model parameters are: N, beta, gamma.

Users can also choose to provide fixed values as the distributional parameter as followed.

sir_model <- denim_dsl({
  S -> I = beta*(I/N)*S
  I -> R = d_exponential(rate = 1/4)
})

Similar to R, users can also add comments in denim DSL by starting the comment with # sign.

sir_model <- denim_dsl({
  # this is a comment
  S -> I = beta*(I/N)*S
  I -> R = d_exponential(rate = 1/4) # this is another comment
})

Run model

To run the model, users must provide:

  • Values for model parameters (in this example, N, beta, and gamma).

  • Initial population for the compartments.

  • Simulation configurations.

Parameters and initial values can be defined as named vectors or named lists in R.

# parameters for the model
parameters <- c(
  beta = 0.4,
  N = 1000,
  gamma = 1/7
)
# initial population for each compartment 
initValues <- c(
  S = 999, 
  I = 50,
  R = 0
)

Simulation configurations are provided as parameters for sim() function which runs the model, where:

  • timeStep is the duration of each time step in the model.

  • simulationDuration is the duration to run the simulation.

mod <- sim(sir_model, 
    parameters = parameters, 
    initialValues = initValues, 
    timeStep = 0.01,
    simulationDuration = 40)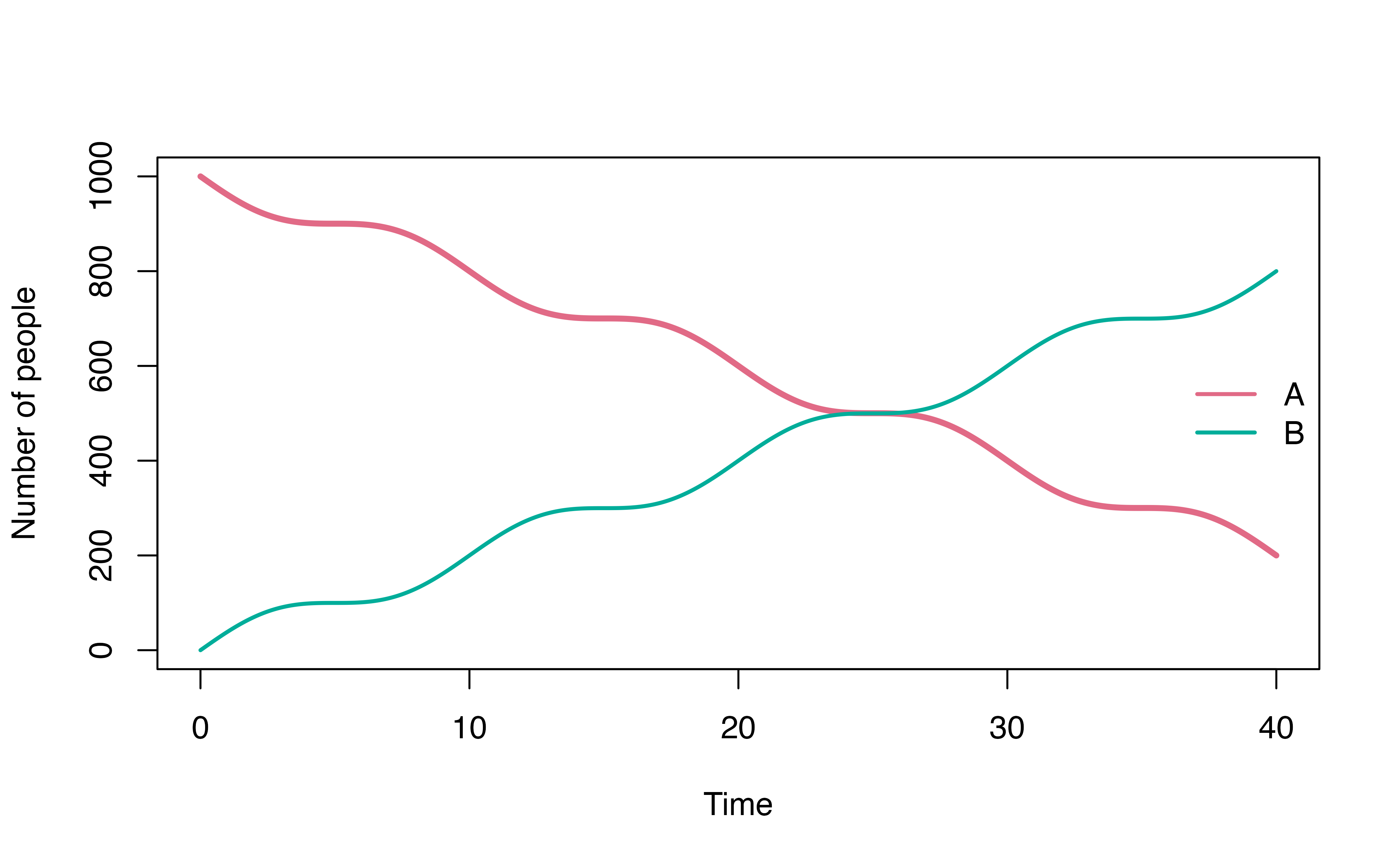
plot(mod, ylim = c(1, 1000))

Time varying transition

variable time is a special variable in denim for time varying transition (e.g. for modeling seasonality). Note that this variable can ONLY be used within math expression.

Example: time varying transition

time_varying_mod <- denim_dsl({
  A -> B = 20 * (1+cos(omega * time)) 
})

# parameters for the model
parameters <- c(
  omega = 2*pi/10
)
# initial population for each compartment 
initValues <- c(A = 1000, B = 0)

mod <- sim(time_varying_mod, 
    parameters = parameters, 
    initialValues = initValues, 
    timeStep = 0.01,
    simulationDuration = 40)

plot(mod, ylim = c(0, 1000))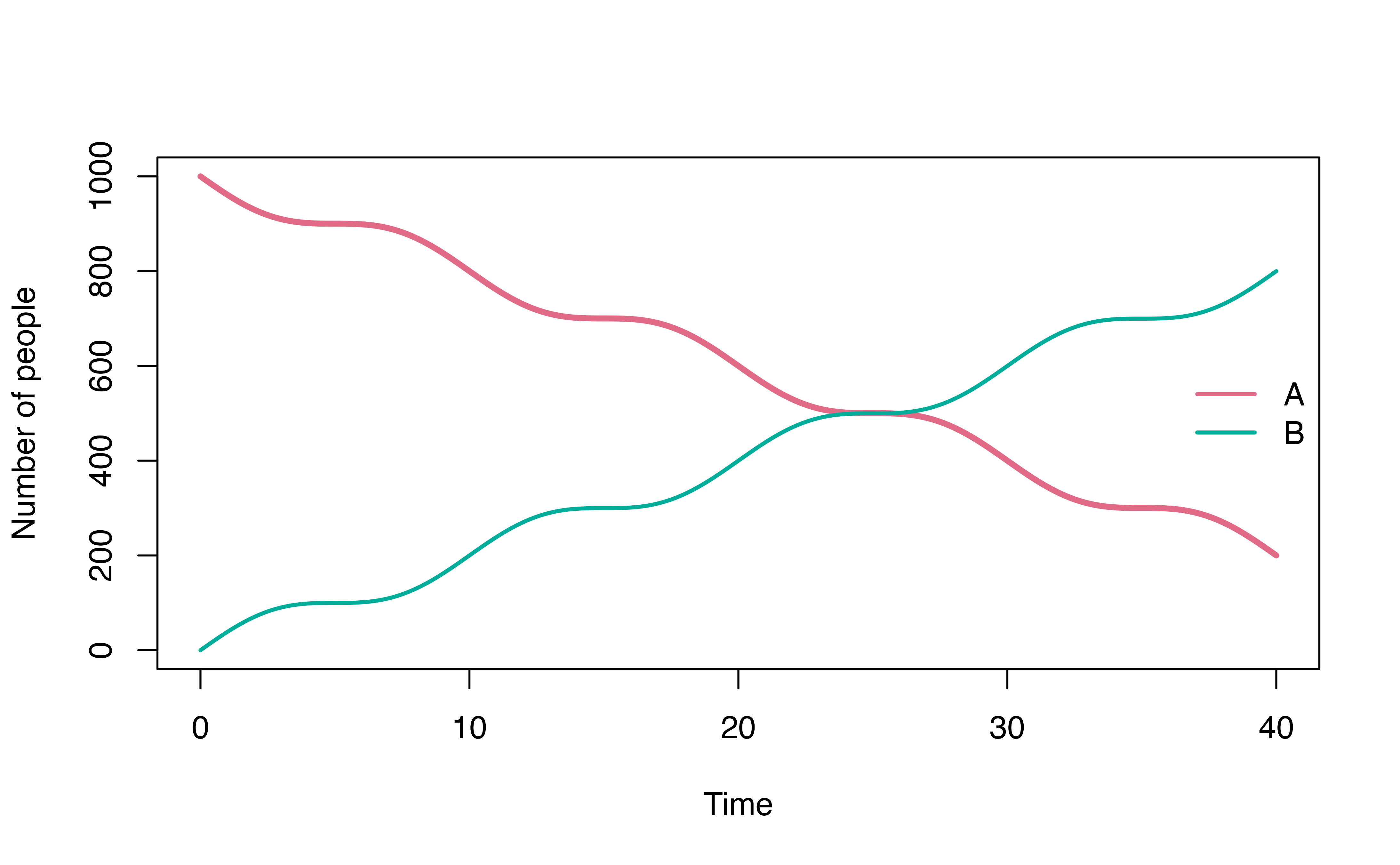

R list

Users can define the model structure directly as a list in R. For example, the SIR model from previous example can be represented as followed.

sir_model_list <- list(
  "S -> I" = "beta * (I/N) * S",
  "I -> R" = d_exponential(rate = "gamma")
)

sir_model_list
#> $`S -> I`
#> [1] "beta * (I/N) * S"
#> 
#> $`I -> R`
#> Discretized exponential distribution
#> Rate = gamma

Note that the transitions (S -> I, I -> R), mathematical expression (beta * (I/N) * S), and the model parameter (gamma) must now be provided as strings.

We can then run the model in the same manner as previously demonstrated.

# parameters for the model
parameters <- c(
  beta = 0.4,
  N = 1000,
  gamma = 1/7
)
# initial population for each compartment 
initValues <- c(
  S = 999, 
  I = 50,
  R = 0
)
# run the simulation
mod <- sim(sir_model_list, 
    parameters = parameters, 
    initialValues = initValues, 
    timeStep = 0.01,
    simulationDuration = 40)
# plot output
plot(mod, ylim = c(1, 1000))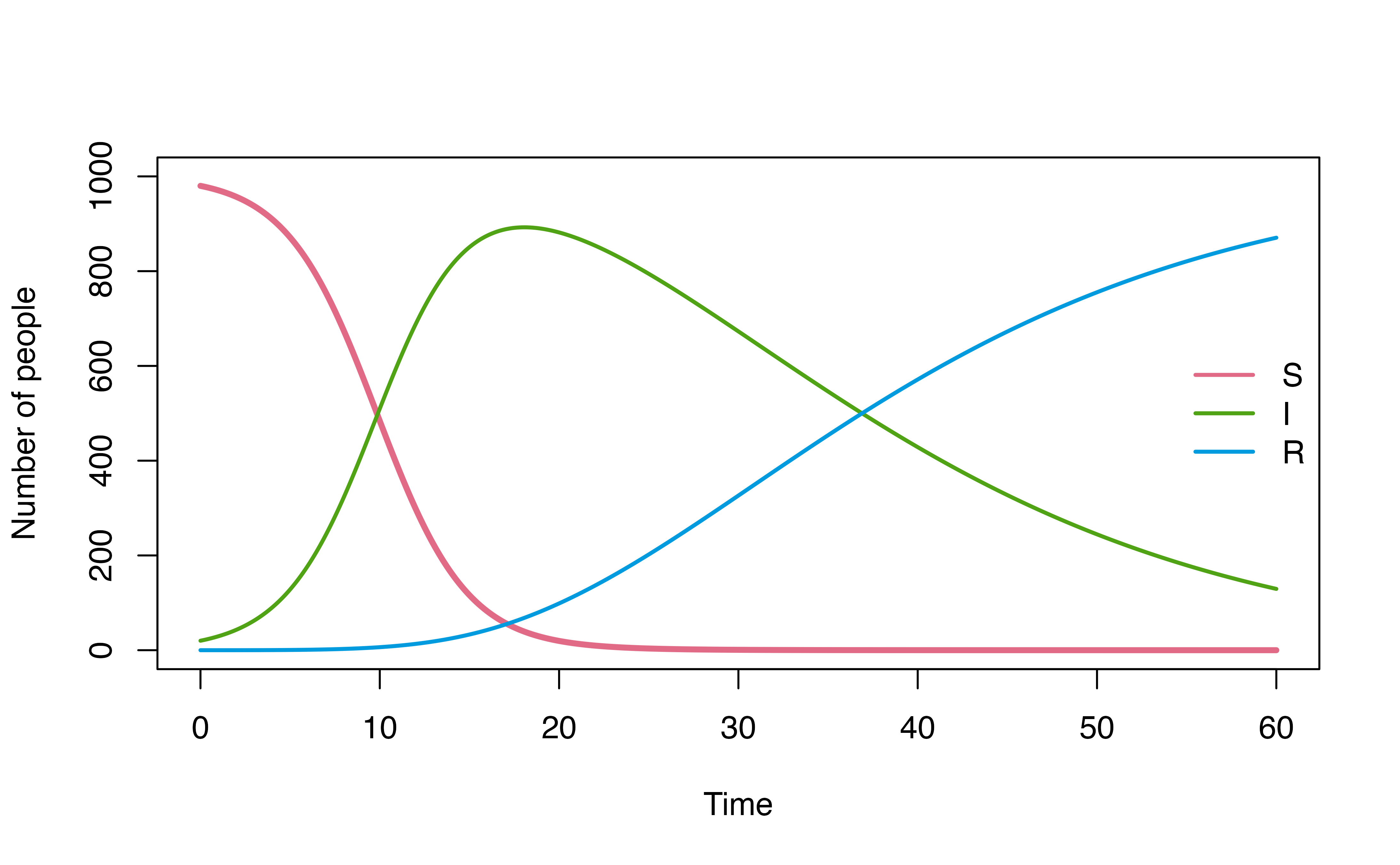

When should I define model as a list in R?

While denim DSL offers cleaner and more readable syntax to define model structure, using R list may be more familiar to R users and better suited for integration to a more R-centric workflow.

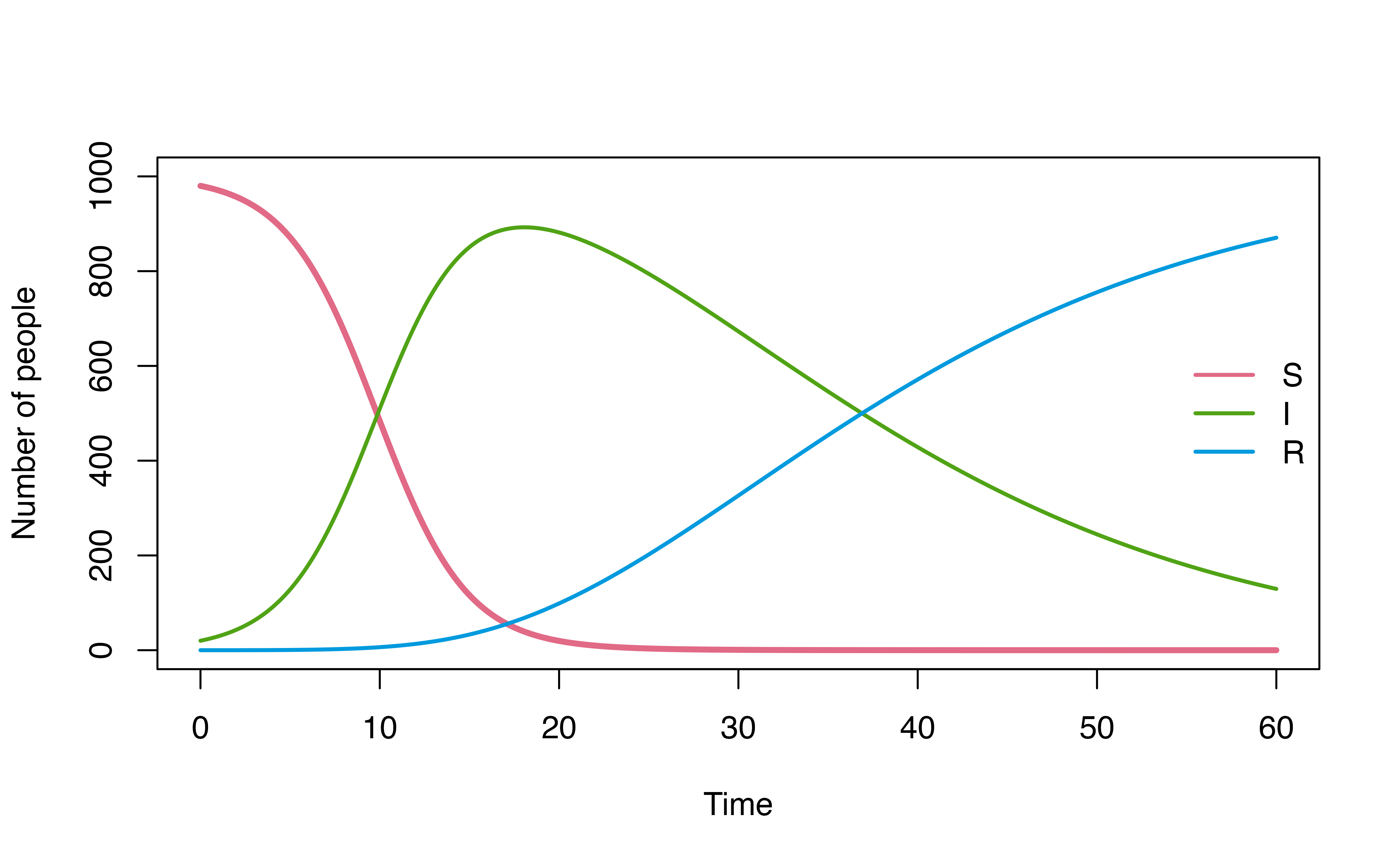
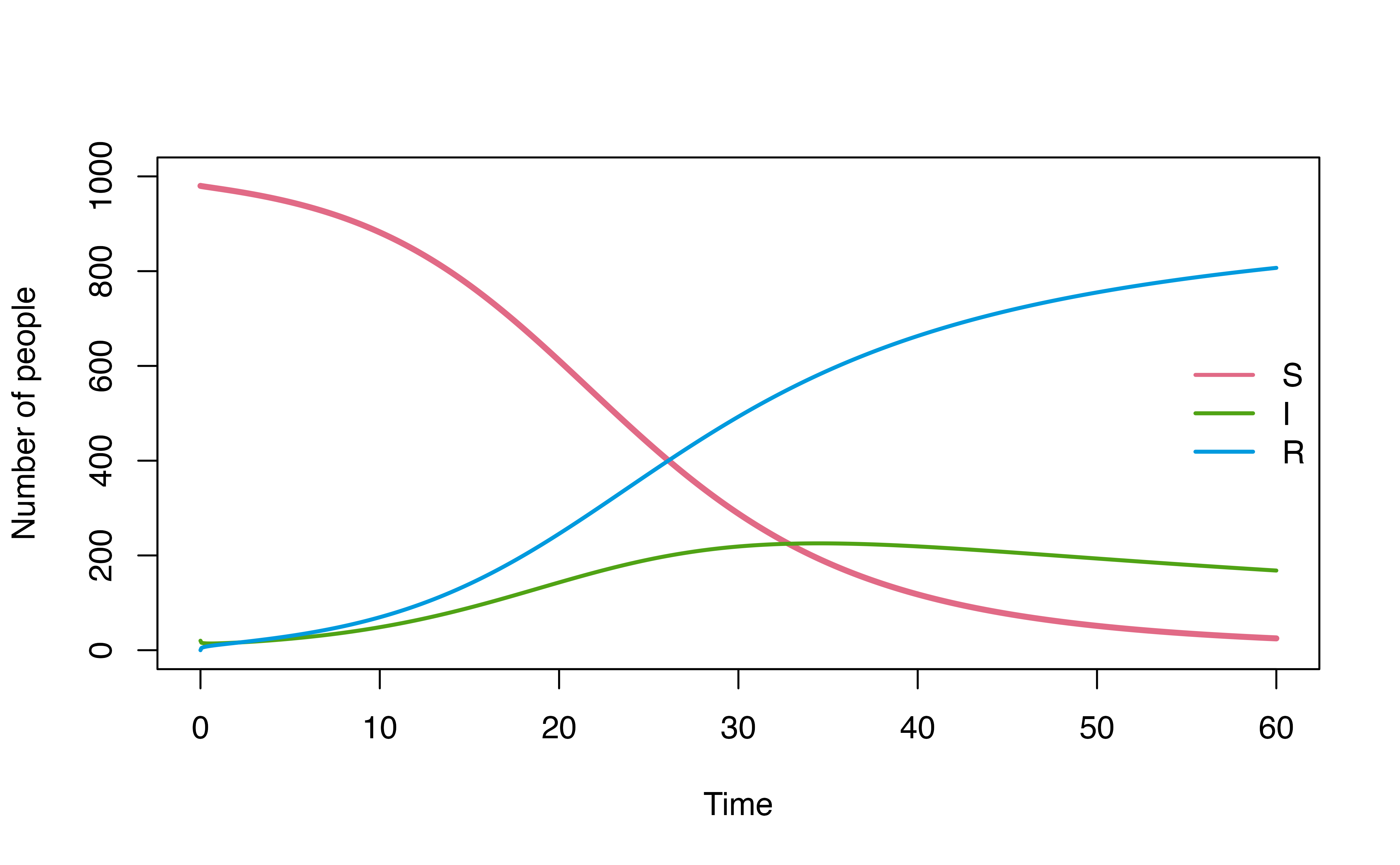
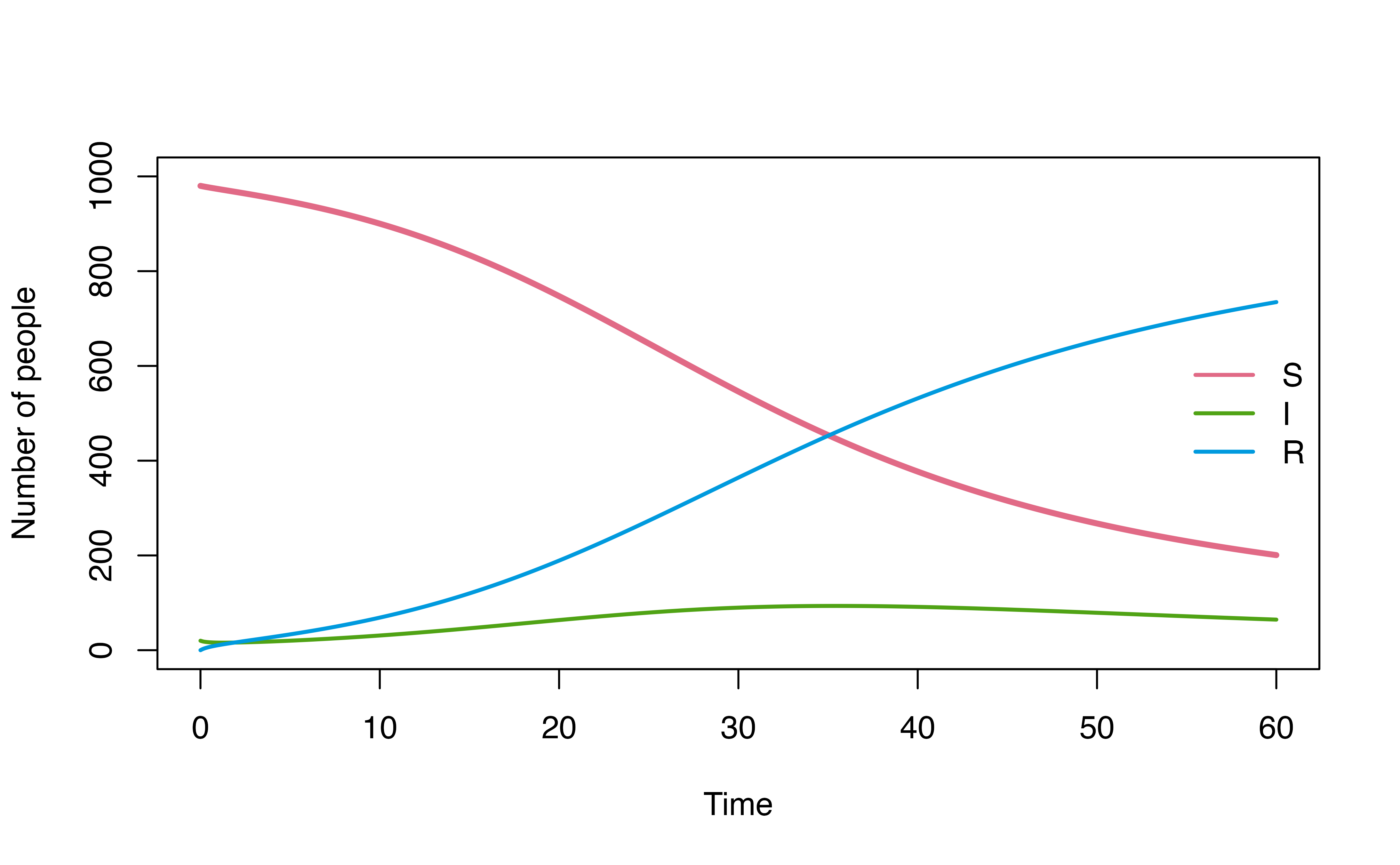
For example, consider a use case below, where we explore how model dynamics change under three different I -> R dwell time distributions (d_gamma, d_weibull, d_lognormal) using map2.

library(tidyverse)
#> Warning: package 'ggplot2' was built under R version 4.3.1
#> Warning: package 'tidyr' was built under R version 4.3.1
#> Warning: package 'readr' was built under R version 4.3.1
#> Warning: package 'purrr' was built under R version 4.3.3
#> Warning: package 'dplyr' was built under R version 4.3.1
#> Warning: package 'stringr' was built under R version 4.3.1
#> Warning: package 'lubridate' was built under R version 4.3.3
# configurations for 3 different I->R transitions
model_config <- tibble(
  IR_dists = c(d_gamma, d_weibull, d_lognormal),
  IR_pars = list(c(rate = 0.1, shape = 3), c(scale = 5, shape = 0.3), c(mu = 0.3, sigma = 2))
)

walk2(
  model_config$IR_dists, model_config$IR_pars, \(dist, par){
    transitions <- list(
      "S -> I" = "beta * S * (I / N)",
      # This is not applicable when using denim_dsl()
      "I -> R" = do.call(dist, as.list(par))
    )
    
    # model settings
    denimInitialValues <- c(S = 980, I = 20, R = 0)
    parameters <- c(
      beta = 0.4,
      N = 1000
    )
    
    # compare output 
    mod <- sim(transitions = transitions, 
               initialValues = denimInitialValues, 
               parameters = parameters, 
               simulationDuration = 60, 
               timeStep = 0.05)
    
    plot(mod, ylim = c(0,1000))
})