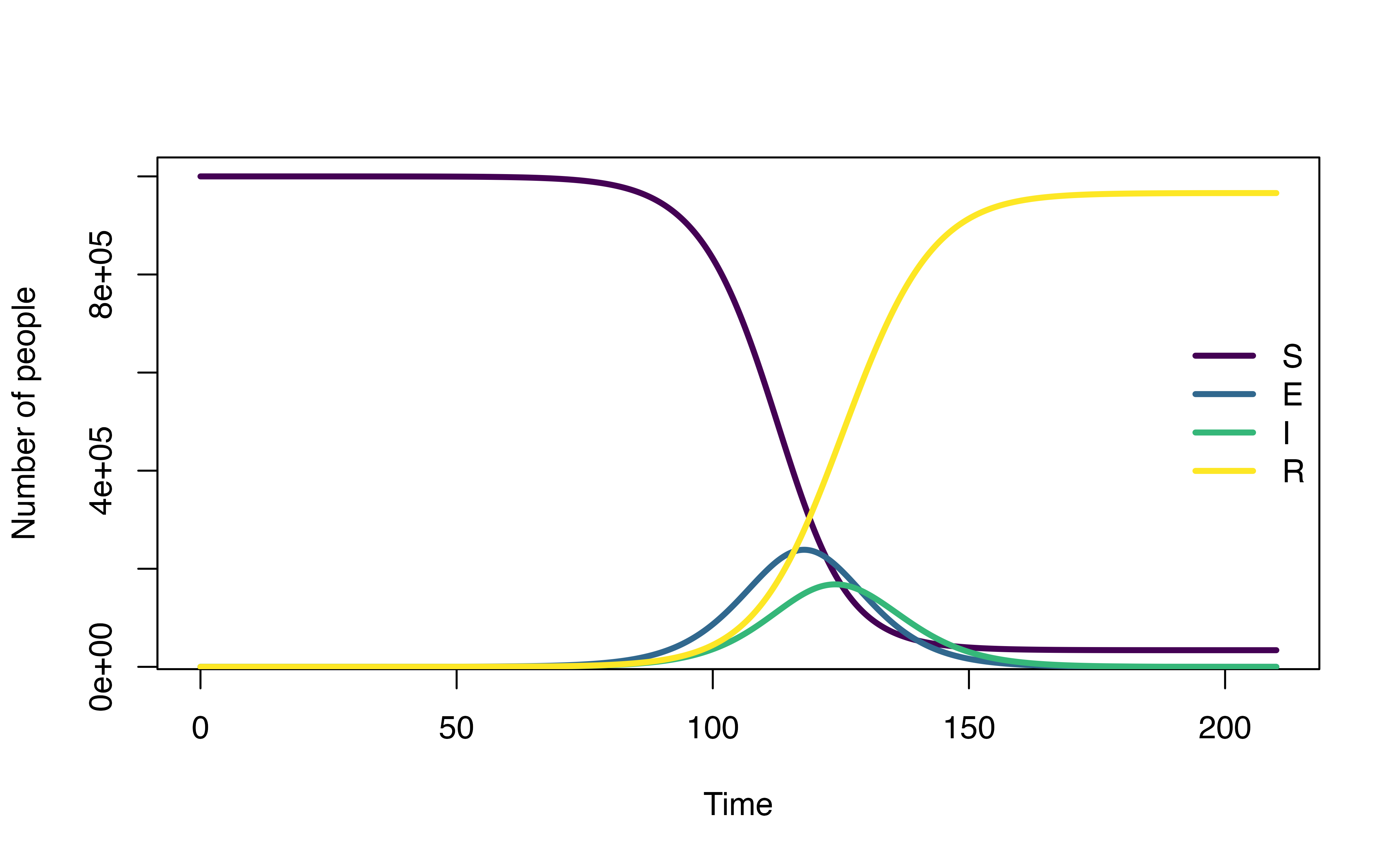denim vs deSolve

Comparison between deSolve and denim

library(denim)
library(deSolve)

## Warning: package 'deSolve' was built under R version 4.3.1

# --- Timestep definition
simulationDuration <- 300 
timestep <- 0.01 # small timestep required for comparison

# --- Transition def for denim
transitions <- list(
  "S -> I" = "beta * S * (I/N) * timestepDur",
  "I -> R" = d_gamma(3, 2)
)
parameters <- c(beta = 0.2, scale = 3, shape=2, N=1000, timestepDur=timestep) 
initialValues <- c(S = 999, I = 1, I1 = 1, I2=0, R=0)

# --- Transition def for deSolve
transition_func <- function(t, state, param){
  with(as.list( c(state, param) ), {
      gamma_rate = 1/scale
      
      dS = - beta * S * I/N
      # apply linear chain trick
      dI1 = beta * S * I/N - gamma_rate*I1
      dI2 = gamma_rate*I1 - gamma_rate*I2
      dI =  dI1 + dI2
      dR = gamma_rate*I2
      list(c(dS, dI, dI1, dI2, dR))
  })
}

Run simulation with denim

denim_runtime <- bench::mark(
  sim(transitions = transitions, initialValues = initialValues, parameters, simulationDuration = simulationDuration, timeStep = timestep),
  iterations = 1
)
denim_runtime <- as.numeric(denim_runtime$total_time)

mod <- sim(transitions = transitions, initialValues = initialValues, parameters, simulationDuration = simulationDuration, timeStep = timestep)
# --- show output
head(mod[mod$Time %in% 1:simulationDuration,])

##     Time        S        I          R
## 101    1 998.7825 1.169597 0.04786644
## 201    2 998.5358 1.296591 0.16756473
## 301    3 998.2665 1.399083 0.33440701
## 401    4 997.9783 1.487980 0.53374794
## 501    5 997.6732 1.569868 0.75697598
## 601    6 997.3521 1.648745 0.99910771

Run simulation with deSolve

times <- seq(0, simulationDuration, timestep)

desolve_runtime <- bench::mark(
  ode(y = initialValues, times = times, parms = parameters, func = transition_func),
  iterations = 1
)

## Warning: Some expressions had a GC in every iteration; so filtering is
## disabled.

desolve_runtime <- as.numeric(desolve_runtime$total_time)

ode_mod <- ode(y = initialValues, times = times, parms = parameters, func = transition_func)

# --- show output
ode_mod <- as.data.frame(ode_mod)
head(ode_mod[ode_mod$time %in% 1:simulationDuration, c("time", "S", "I", "R")])

##     time        S        I         R
## 101    1 998.7824 1.169731 0.0479167
## 201    2 998.5355 1.296752 0.1677463
## 301    3 998.2660 1.399189 0.3347737
## 401    4 997.9777 1.487967 0.5343309
## 501    5 997.6725 1.569688 0.7577887
## 601    6 997.3515 1.648357 1.0001499

Execution time comparison

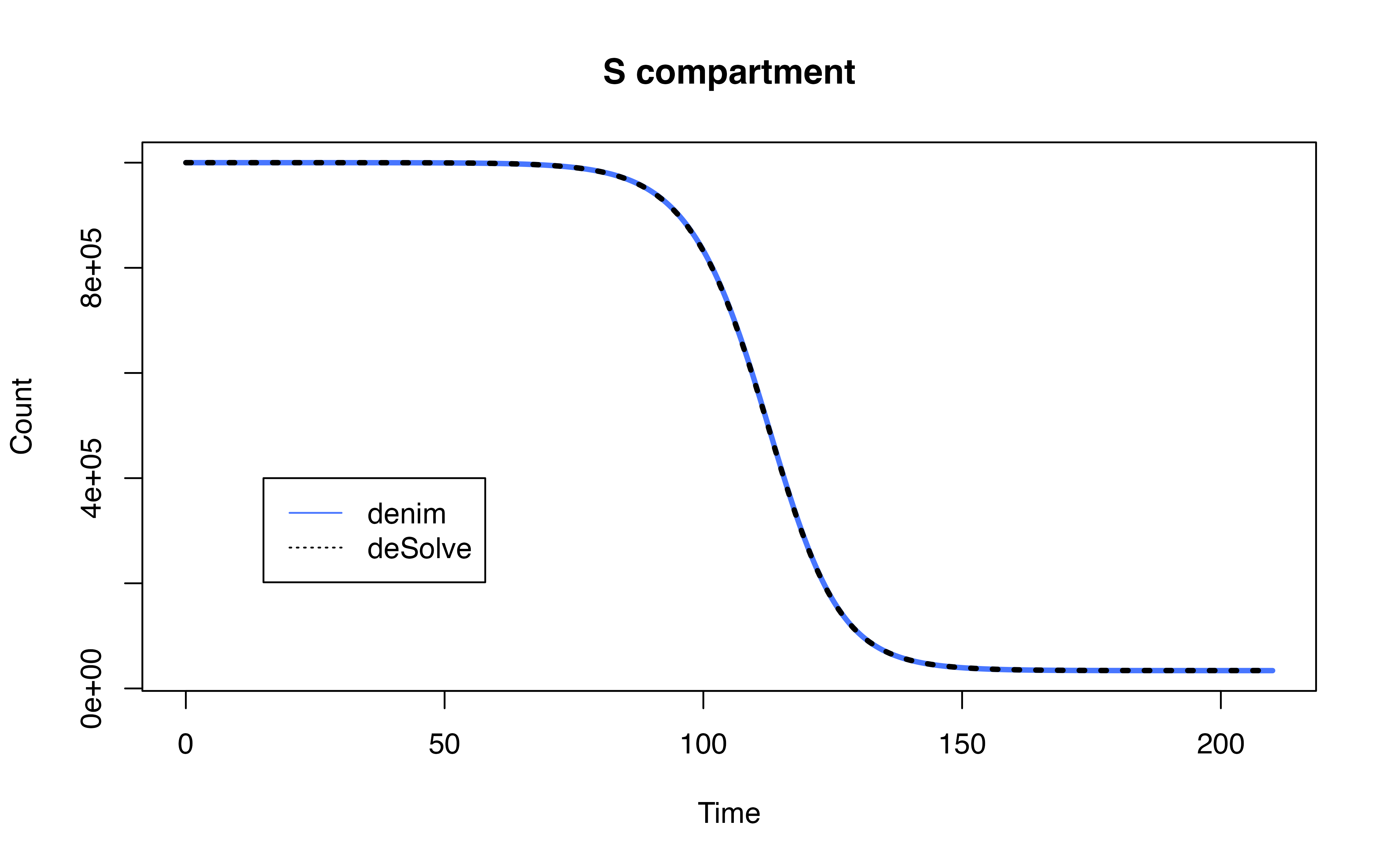
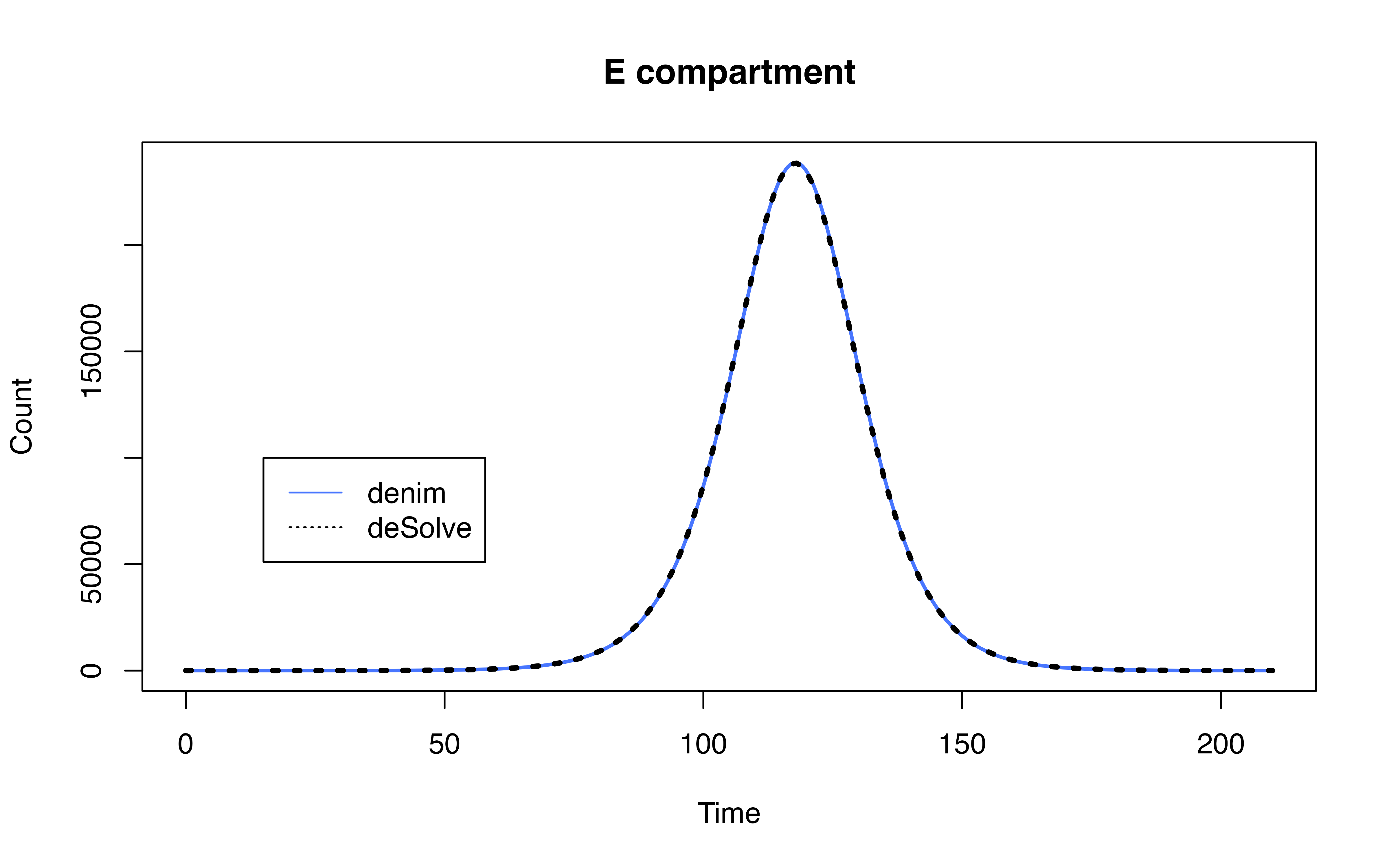
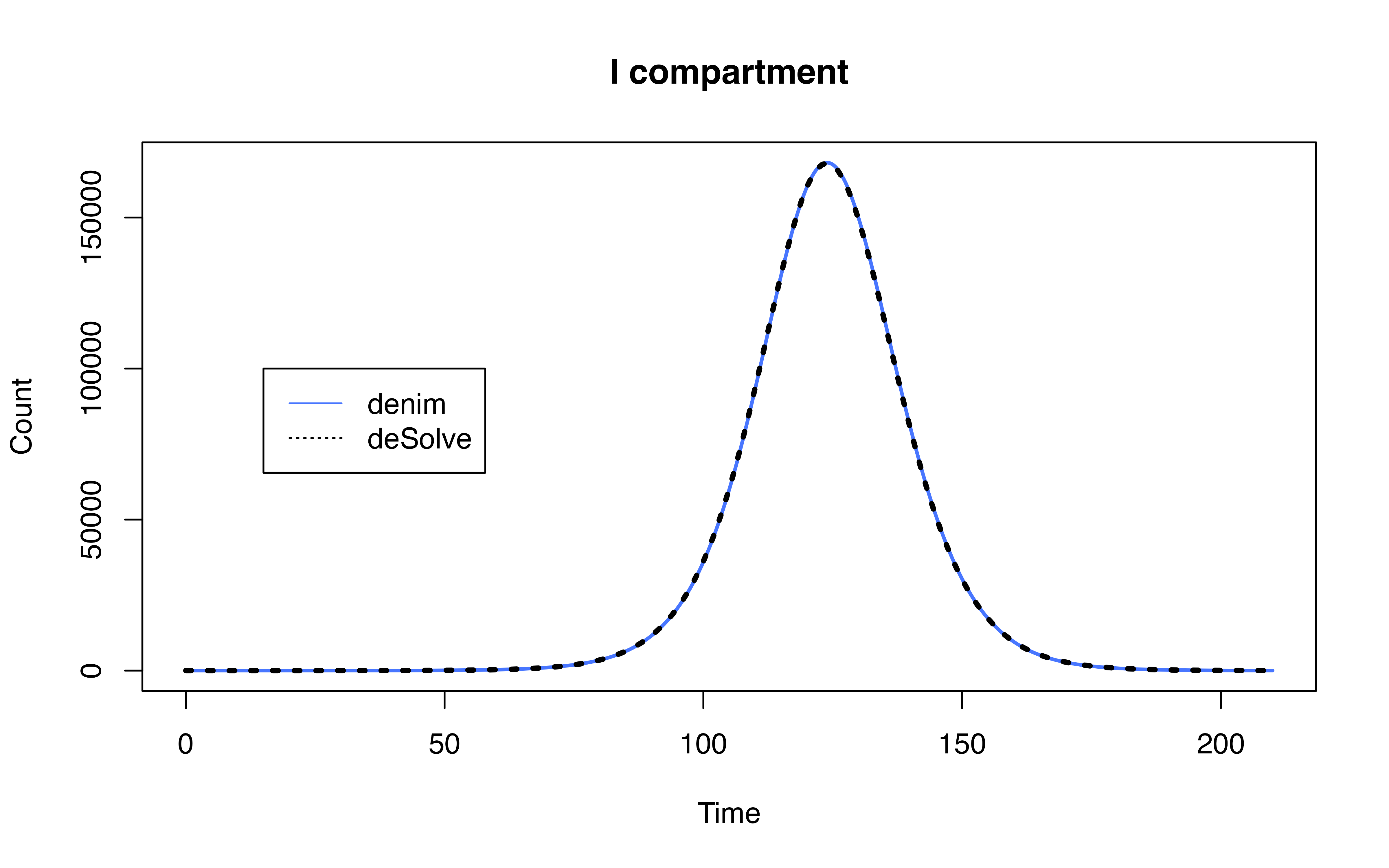
denim takes approximately 4.3 times as long as deSolve to compute the result with the given specifications .

This significant difference can be attributed to the difference in approaches: deSolve solves a system of ODEs while denim iterates through each timestep and updates the population in each compartment

While the approach in denim allow more flexibility in types of dwell time distributions, the computation time scales up as timestep grows smaller (in O(n) time complexity).

Plot the result

# increase timestep before plotting
mod <- mod[mod$Time %in% seq(0, simulationDuration, 0.2),]
ode_mod <- ode_mod[ode_mod$time %in% seq(0, simulationDuration, 0.2),]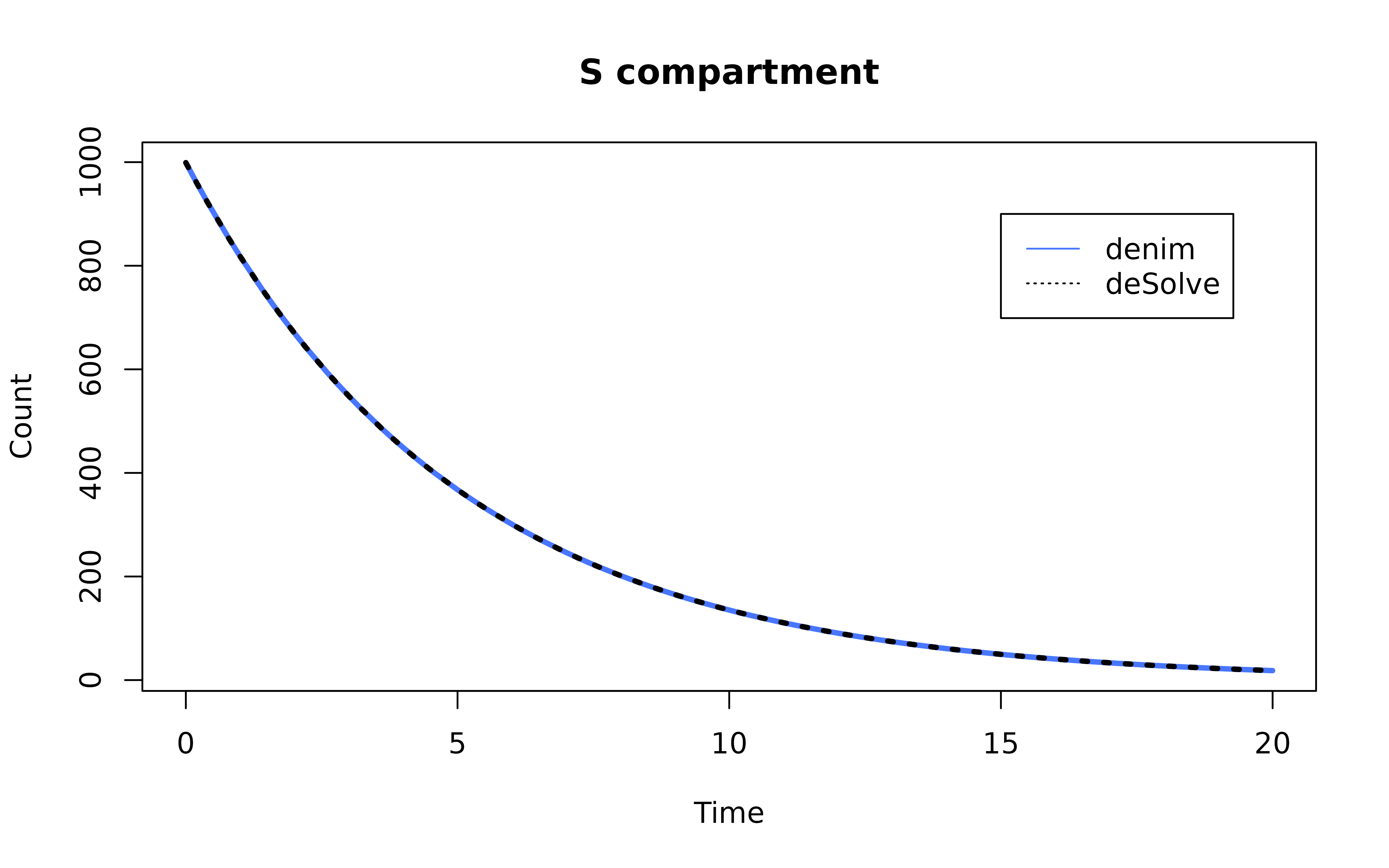

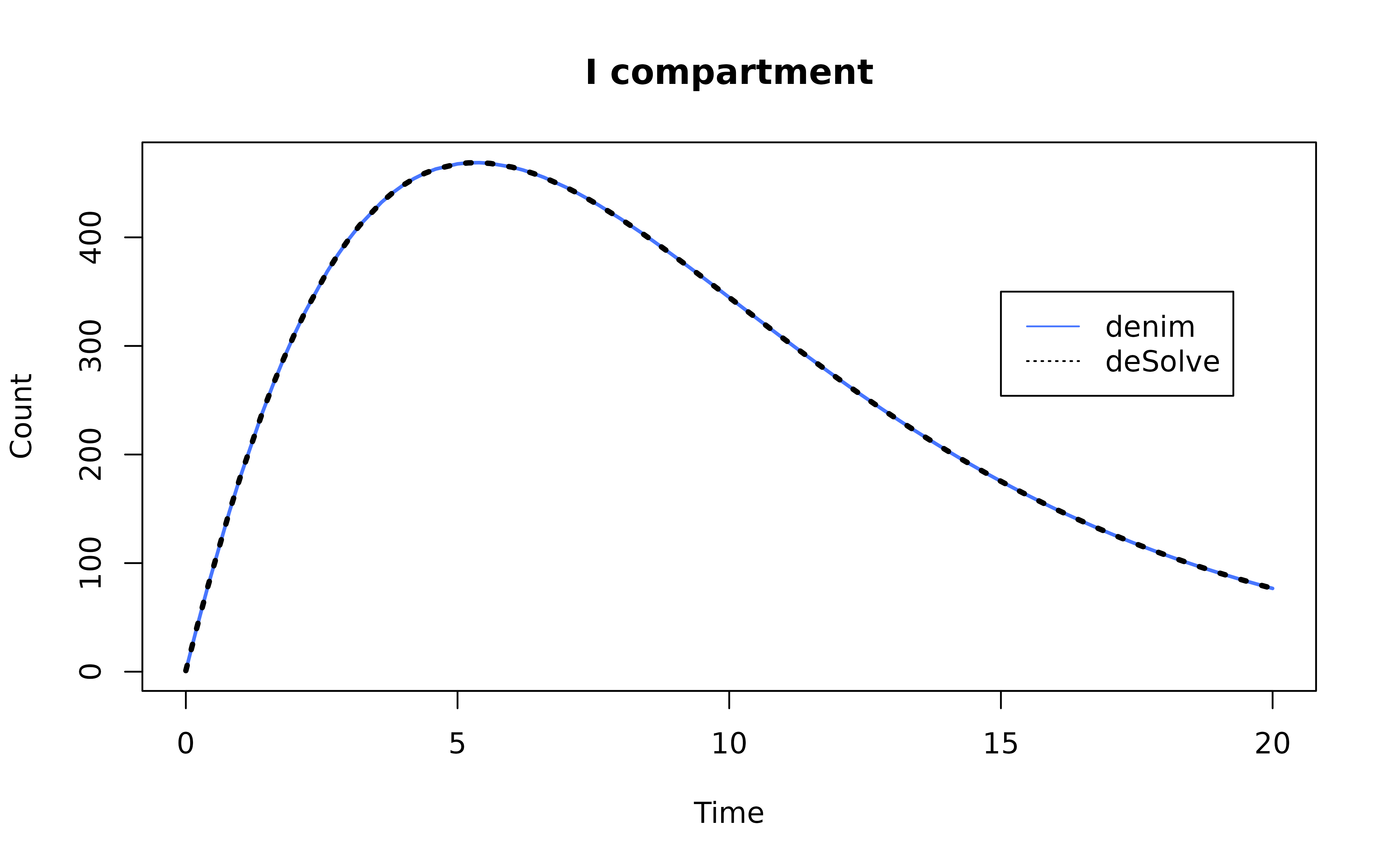
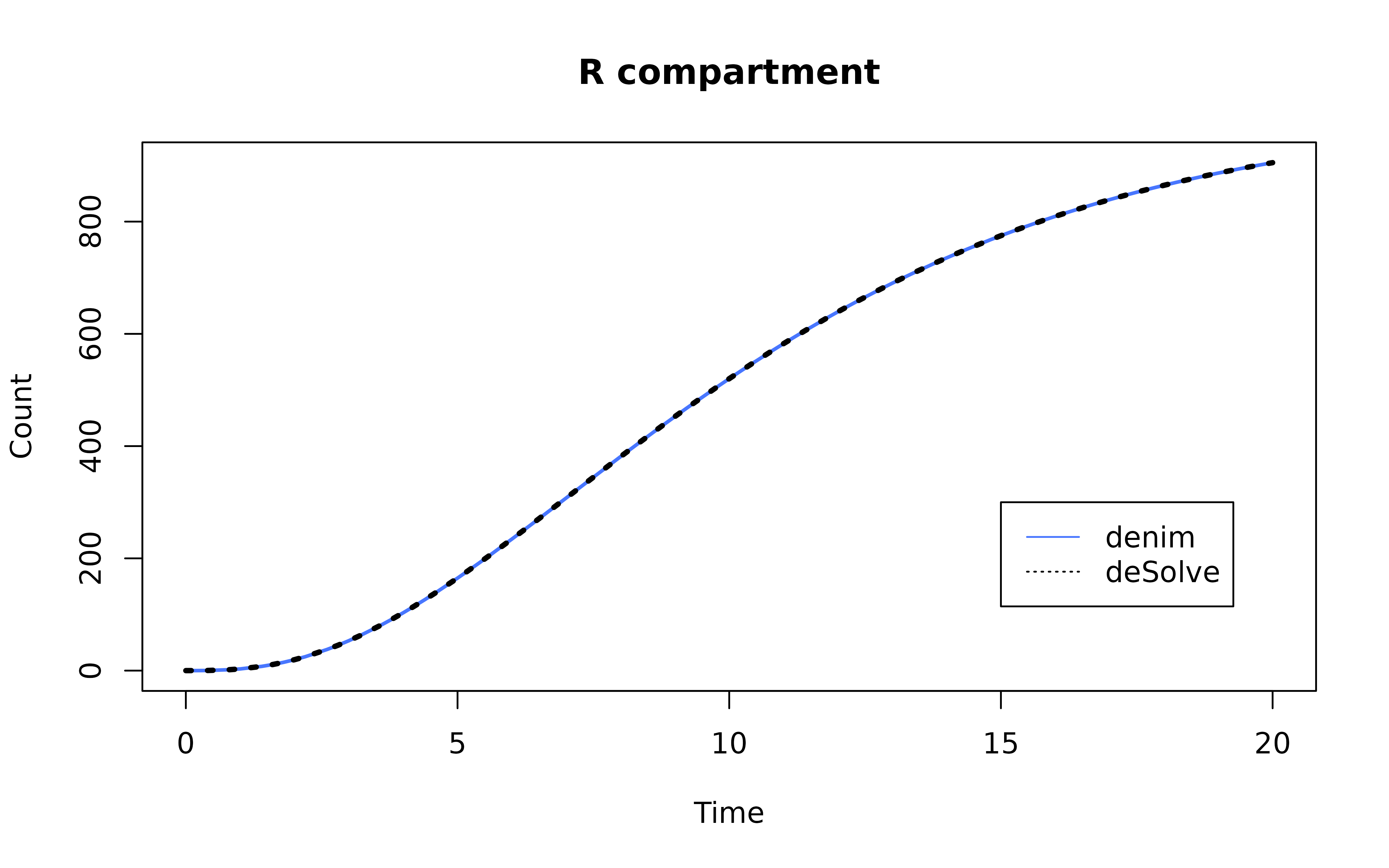
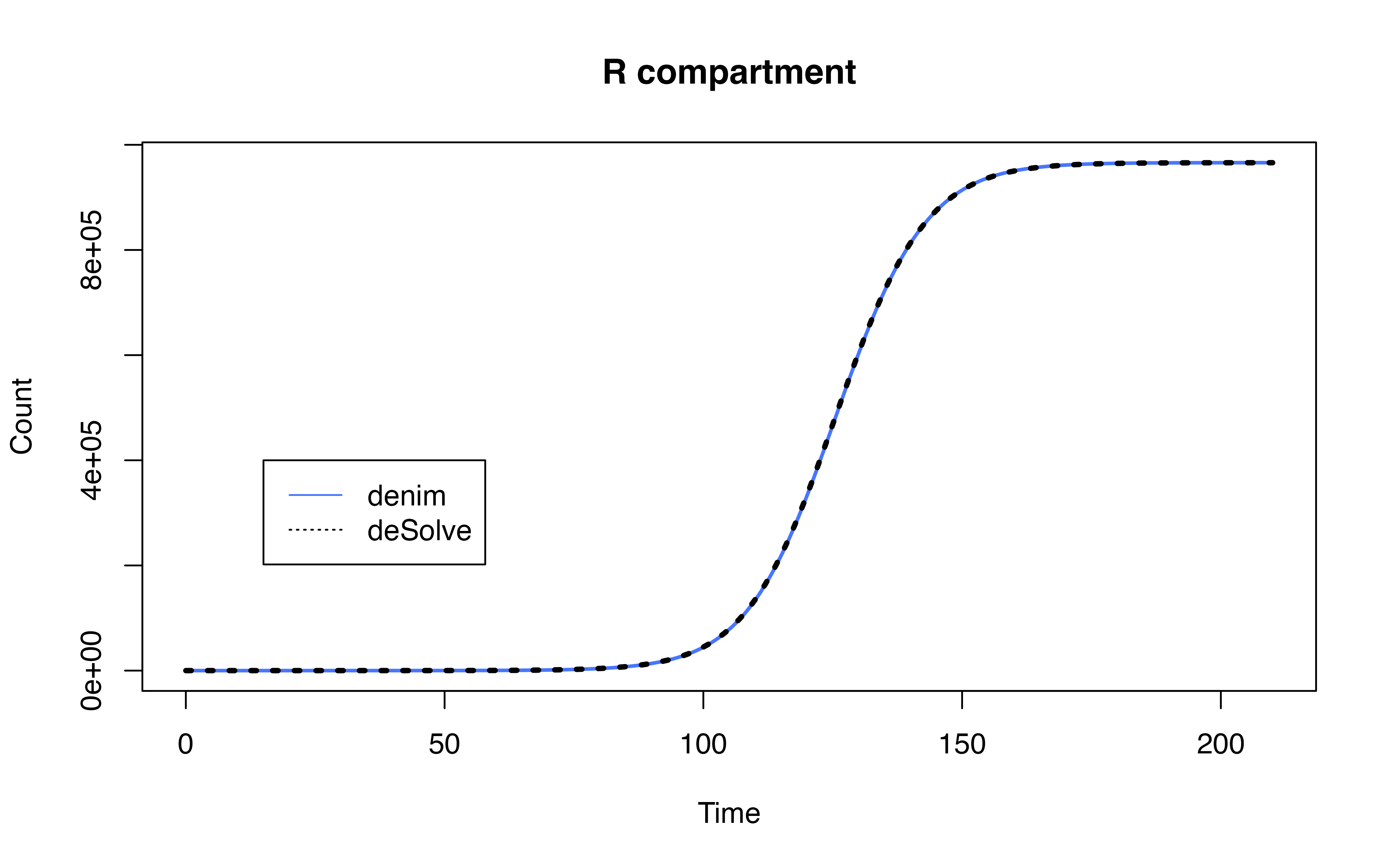
Comparison with SEIR model

Implementation using deSolve

model definition deSolve

library(deSolve)
parameters <- c(scale_I = 4, shape_I=2,
                scale_R = 3, shape_R = 2,
                timeStepDur = 1, R0 = 3.5, N = 1e6) 
initialValues <- c(S = 999999, E1 = 1,
                   E2 = 0, E = 0, I1=0, 
                   I2=0, I=0, R=0
                   )

# --- Transition def for deSolve
transition_func <- function(t, state, param){
  with(as.list( c(state, param) ), {
      gamma_rate_I = 1/scale_I
      gamma_rate_R = 1/scale_R
      
      tr = scale_R*shape_R
      
      dS = - (R0/tr) * S * I/N
      # apply linear chain trick
      dE1 = (R0/tr) * S * I/N - gamma_rate_I*E1
      dE2 = gamma_rate_I*E1 - gamma_rate_I*E2
      dE = dE1 + dE2
      dI1 = gamma_rate_I*E2 - gamma_rate_R*I1
      dI2 = gamma_rate_R*I1 - gamma_rate_R*I2
      dI =  dI1 + dI2

      dR = gamma_rate_R*I2
      list(c(dS, dE1, dE2, dE, dI1, dI2, dI, dR))
  })
}

times <- seq(0, 210, 1)

ode_mod <- ode(y = initialValues, times = times, parms = parameters, func = transition_func)

# --- show output
ode_mod <- as.data.frame(ode_mod)

Implementation using denim

model definition in denim

denim_model <- list(
  "S -> E" = "(R0/tr) * timeStepDur * S * (I/N)", # formulate according that of uSEIR method
  "E -> I" = d_gamma(scale = 4, shape = 2),
  "I -> R" = d_gamma(scale = 3, shape = 2)
)

initialValues <- c(S = 999999, E = 1, I= 0, R= 0)
parameters <- c(R0 = 3.5, 
                tr = 3*2, # compute mean recovery time, for gamma it's scale*shape
                N = 1e6, timeStepDur = 0.01)

mod <- sim(transitions = denim_model, 
                     initialValues = initialValues,
                     parameters = parameters,
                     simulationDuration = 210, timeStep = 0.01)

# denim_out[, c("S","E", "I", "R")] <- denim_out[, c("S","E", "I", "R")]/1e6
plot(mod)