10  Estimating \(R_0\)

Preparation

Download COVID-19 incidence data here:

There are 2 approaches to estimating \(R_0\), depending on the type of data available:

1. Individual-level modelling: used when individual-level data (e.g. contact tracing) is available and is often considered prospective (Pandit, 2020).

2. Population-level modelling: used when population-level data (e.g. incidence) is available and is often considered retrospective (Pandit, 2020).

The 2 approaches may produce very different numbers because:

• Individual-level calculates the value of \(R_0\), while the population-level calculates the value of a threshold parameter (Breban et al., 2007).
• Individual-level assumes a social contact network with a structure that is different from the all-to-all network assumed by ODE models (Breban et al., 2007).
• Population-level predictions based upon an ODE model that use the \(R_0\) value from contact tracing as a threshold parameter may be inaccurate. Only an epidemic threshold (from population-level modelling) can be used to design control strategies (Breban et al., 2007).
• \(R_0\) value from contact tracing is useful in conjunction with population-level epidemic data to understand the possible transmission mechanisms of the epidemic at the individual-level.

10.1 Contact tracing

Contact tracing figure from (Bradshaw et al., 2021)

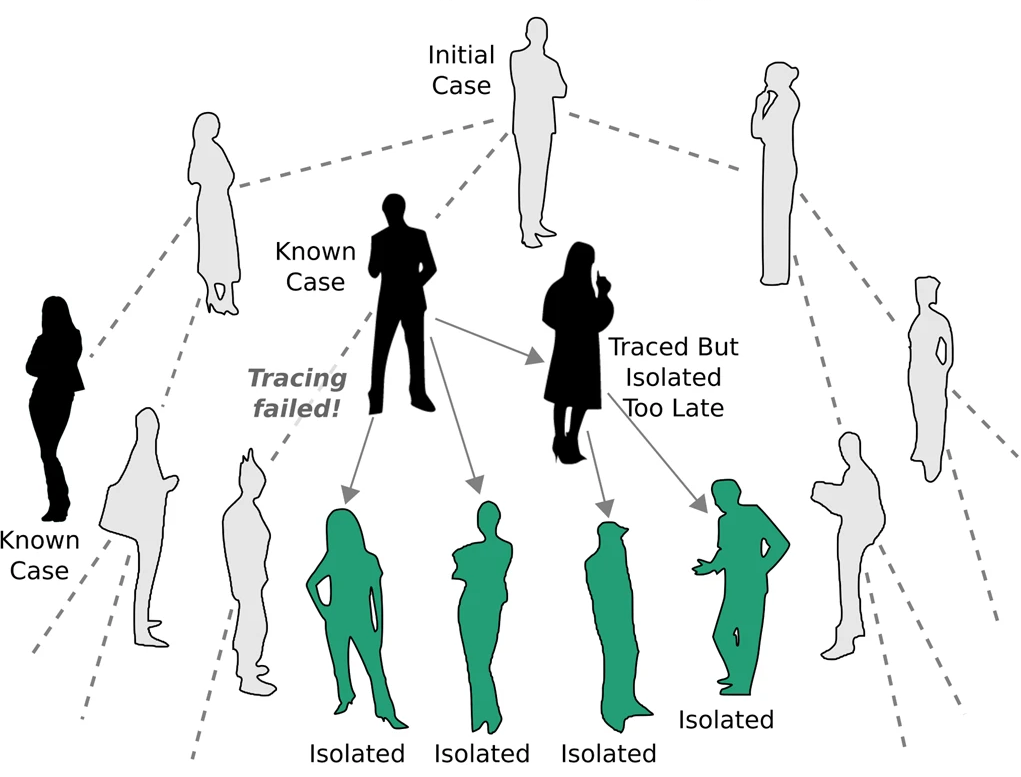
This approach is based upon the definition of \(R_0\). Once an individual is diagnosed, his/her contacts are traced and tested. \(R_0\) is then computed by averaging over the number of secondary cases of many diagnosed individuals (Breban et al., 2007).

10.2 Population-level

10.2.1 Exponential growth rate

Step 1. Find an estimate for the mean generation time \(T_g\).

Step 2. Identify the exponential phase of the epidemic curve: the period of which \(\log(\text{incidence})\) is linear.

Step 3. Estimate the growth rate \(r\) for that phase by finding the slope from the linear regression on the \(\log(\text{incidence})\).

Proof

See Section 4 for more details. During the exponential phase, the incidence at time \(t\) is given by:

\[C_t = C_0 e^{rt}\]

Take the natural logarithm:

\[\log C_t = log C_0 + rt\]

Therefore \(r\) is the slope from the linear regression on the \(\log(\text{incidence})\).

Step 4. Given the exponential growth rate \(r\) and the \(T_g\), calculate the basic reproduction number:

• Discrete generation:

\[R_0 = e^{rT_g}\]

• In an SIR model \(T_g = \frac{1}{\gamma}\) so:

\[R_0 \approx 1 + rD = 1 + \frac{r}{\gamma}\]

• In an SEIR model \(T_g = \frac{1}{\gamma} + \frac{1}{\sigma}\) so:

\[R_0 \approx (1 + rD)(1 + rL) = \left( 1 + \frac{r}{\gamma} \right) \left( 1 + \frac{r}{\sigma} \right)\]

In which:

• \(D\) is the mean duration of the infectiousness.
• \(L\) is the mean duration of latency.

10.2.2 Code

library(ggplot2)
library(patchwork)

Read the data

df <- read.csv("data/covid_uk.csv")

ggplot(df, aes(x = day, y = inc)) +
  geom_point() +
  labs(x = "Day", y = "Incidence") +
  theme_minimal()

Step 1. Find an estimate for the mean generation time \(T_g\). Let say \(T_g = D = 6.6\) for COVID-19.

Step 2. Identify the exponential phase of the epidemic curve: the period of which \(\log(\text{incidence})\) is linear.

df$loginc <- log(df$inc)

p1 <- ggplot(df, aes(x = day, y = inc)) +
  geom_point() +
  labs(x = NULL, y = "Incidence") +
  theme_minimal()

p2 <- ggplot(df, aes(x = day, y = loginc)) +
  geom_point() +
  labs(x = "Day", y = "Log incidence") +
  theme_minimal()

p1 / p2

Looks like day 1 to 21 is the exponential phase.

Step 3. Estimate the growth rate \(r\) for that phase by finding the slope from the linear regression on the \(\log(\text{incidence})\).

mod <- lm(loginc ~ day, data = df[1:21,])
pred <- data.frame(day = 1:21, loginc = predict(mod, data = df[1:21,]))

ggplot(df, aes(x = day, y = loginc)) +
  geom_point() +
  geom_line(data = pred, color = "blue") +
  labs(x = "Day", y = "Log incidence") +
  theme_minimal()

Look at the linear regression:

summary(mod)

Call:
lm(formula = loginc ~ day, data = df[1:21, ])

Residuals:
     Min       1Q   Median       3Q      Max 
-1.45946 -0.32865 -0.05379  0.36148  0.98657 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.38285    0.25339  -1.511    0.147    
day          0.30705    0.02018  15.216 4.28e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.56 on 19 degrees of freedom
Multiple R-squared:  0.9242,    Adjusted R-squared:  0.9202 
F-statistic: 231.5 on 1 and 19 DF,  p-value: 4.28e-12

The slope is 0.3070509.

Step 4. Given the exponential growth rate \(r\) and the \(T_g\), calculate the basic reproduction number.

Discrete generation: \(R_0 = e^{rT_g}\)

exp(unname(mod$coefficients[2]) * 6.6)

[1] 7.587758

SIR model: \(R_0 \approx 1 + rD\)

1 + unname(mod$coefficients[2]) * 6.6

[1] 3.026536

\(R_0\) estimates are affected by the mean, variance and shape of the generation time distribution.

• A larger mean \(T_g\) leads to larger \(R_0\).
• For the 2 models with the same mean but different distributions \(T_g\), \(R_0\) estimates are different:
  • Discrete generation assumes a uniform \(T_g\).
  • SIR model assumes an exponential \(T_g\).

Package R0 provide a ready-to-use function est.R0.EG() to estimate \(R_0\) using exponential growth rate method. We can define different shape of \(T_g\), let try a \(\Gamma(6.6, 4)\):

library(R0)
gt <- generation.time("gamma", c(6.6, 4))
plot(gt)

Now compute \(R_0\):

est.R0.EG(df$inc, gt, begin = 1, end = 21)

Waiting for profiling to be done...

Reproduction number estimate using  Exponential Growth  method.
R :  3.949484[ 3.716905 , 4.198451 ]

10.2.3 Simple compartmental models

Consider a simple closed population SIR model.

\[\begin{align} \frac{dS}{dt} & = -\beta SI \\ \frac{dI}{dt} & = \beta SI - \gamma I\\ \frac{dR}{dt} & = \gamma I \end{align}\]

Focusing on the \(I\) equation:

\[\frac{dI}{dt} = \beta SI - \gamma I = I (\beta S - \gamma)\]

A disease spreads when:

\[\begin{align} \frac{dI}{dt} & > 0 \\ \Leftrightarrow I (\beta S - \gamma) & > 0 \\ \Leftrightarrow \beta S - \gamma & > 0 \\ \Leftrightarrow \beta S & > \gamma \\ \Leftrightarrow \frac{\beta S}{\gamma} & > 1 \end{align}\]

This leads to the definition of \(R_0\). By Definition 1, \(R_0\) is the \(R\) in a fully susceptible population \(S_0\):

\[R_0 = \frac{\beta S_0}{\gamma}\]

Therefore:

• \(R_0 > 1\) meaning that \(\frac{dI}{dt} > 0\), then the disease will spread.
• \(R_0 < 1\) meaning that \(\frac{dI}{dt} < 0\), then no epidemic occurs.

For more complex compartmental models, especially those with more infected compartments, as proposed by (Diekmann et al., 1990) and (Driessche & Watmough, 2002), \(R_0\) can be determined using the next generation matrix (Driessche, 2017).

10.2.4 Next generation matrix

\(R_0\) is the maximum absolute eigenvalue (also called the spectral radius) of the next generation matrix (NGM) (Driessche, 2017).

Consider an SEIR model with equal birth and death rate \(\mu\).

\[\begin{align} \frac{dS}{dt} & = \mu (S + E + I + R) -\beta SI - \mu S \\ \frac{dE}{dt} & = \beta SI - \sigma E - \mu E \\ \frac{dI}{dt} & = \sigma E - \gamma I - \mu I \\ \frac{dR}{dt} & = \gamma I - \mu R \end{align}\]

Step 1. Identify the infected compartments

For our SEIR model, the infected compartments are \(E\) and \(I\).

Step 2. Write the NGM functions

• \(\mathcal{F}_i(x)\): is the rate of appearance of new infections in compartment \(i\) (Driessche, 2017) (caused by contact).
• \(\mathcal{V}_i(x)\): is the rate of other transitions between compartment \(i\) and other infected compartments (Driessche, 2017) (caused by transition between compartments).

For our SEIR model, we would write \(\mathcal{F}\) and \(\mathcal{V}\) as follows:

\[\mathcal{F} = \begin{bmatrix} \beta SI \\ 0 \end{bmatrix}\] \(\mathcal{F}\) is a vector contains of \(\begin{bmatrix} \mathcal{F}_1 \\ \mathcal{F}_2 \end{bmatrix}\):

• \(\mathcal{F}_1 = \beta SI\): the rate of new infections (caused by contact) in compartment \(E\).
• \(\mathcal{F}_2 = 0\): as there is no new infections (caused by contact) in compartment \(I\).

\[\mathcal{V} = \begin{bmatrix} \sigma E + \mu E \\ - \sigma E + \gamma I + \mu I \end{bmatrix}\]

\(\mathcal{V}\) is a vector contains of \(\begin{bmatrix} \mathcal{V}_1 \\ \mathcal{V}_2 \end{bmatrix}\):

• \(\mathcal{V}_1 = \sigma E + \mu E\): is the rate of other transitions to and from compartment \(E\).
• \(\mathcal{V}_2 = - \sigma E + \gamma I + \mu I\): is the rate of other transitions to and from compartment \(I\).

\(\mathcal{F}\) and \(\mathcal{V}\) are written such that:

\[\frac{dx}{dt} = \mathcal{F} - \mathcal{V}\]

Here we have:

\[\frac{dE}{dt} = \mathcal{F}_1 - \mathcal{V}_1 = \beta SI - (\sigma E + \mu E)\]

\[\frac{dI}{dt} = \mathcal{F}_2 - \mathcal{V}_2 = 0 - (- \sigma E + \gamma I + \mu I)\]

Step 3. Find the Jacobian matrix

Jacobian matrix \(F\) for \(\mathcal{F}\), and \(V\) for \(\mathcal{V}\). Jacobian matrix is a matrix contain all partial derivatives of a vector function.

\[\begin{align} F & = \begin{bmatrix} \frac{\partial \mathcal{F}_1}{\partial E} & \frac{\partial \mathcal{F}_1}{\partial I} \\ \frac{\partial \mathcal{F}_2}{\partial E} & \frac{\partial \mathcal{F}_2}{\partial I} \end{bmatrix} \\ & = \begin{bmatrix} \frac{\partial [\beta SI]}{\partial E} & \frac{\partial [\beta SI]}{\partial I} \\ \frac{\partial [0]}{\partial E} & \frac{\partial [0]}{\partial I} \end{bmatrix} \\ & = \begin{bmatrix} 0 & \beta S \\ 0 & 0 \end{bmatrix} \end{align}\]

In which:

• \(\frac{\partial [\beta SI]}{\partial E} = 0\): because there is no \(E\) in \(\beta SI\).
• \(\frac{\partial [\beta SI]}{\partial I} = \beta S\).

\[\begin{align} V & = \begin{bmatrix} \frac{\partial \mathcal{V}_1}{\partial E} & \frac{\partial \mathcal{V}_1}{\partial I} \\ \frac{\partial \mathcal{V}_2}{\partial E} & \frac{\partial \mathcal{V}_2}{\partial I} \end{bmatrix} \\ & = \begin{bmatrix} \frac{\partial [\sigma E + \mu E]}{\partial E} & \frac{\partial [\sigma E + \mu E]}{\partial I} \\ \frac{\partial [- \sigma E + \gamma I + \mu I]}{\partial E} & \frac{\partial [- \sigma E + \gamma I + \mu I]}{\partial I} \end{bmatrix} \\ & = \begin{bmatrix} \sigma + \mu & 0 \\ - \sigma & \gamma + \mu \end{bmatrix} \end{align}\]

Step 4. Compute the NGM

Use Definition A.12 to compute inverse matrix \(V^{-1}\):

\[\begin{align} V^{-1} & = \frac{1}{(\sigma + \mu)(\gamma + \mu)} \begin{bmatrix} \gamma + \mu & - 0 \\ - \sigma & \sigma + \mu \end{bmatrix} \\& = \begin{bmatrix} \frac{1}{\sigma + \mu} & 0 \\ \frac{\sigma}{(\sigma + \mu)(\gamma + \mu)} & \frac{1}{\gamma + \mu} \end{bmatrix} \end{align}\]

\[\begin{align} K & = FV^{-1} \\ & = \begin{bmatrix} 0 & \beta S \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sigma + \mu} & 0 \\ \frac{\sigma}{(\sigma + \mu)(\gamma + \mu)} & \frac{1}{\gamma + \mu} \end{bmatrix} \\ & = \begin{bmatrix} \frac{\beta S \sigma}{(\sigma + \mu)(\gamma + \mu)} & \frac{\beta S}{\gamma + \mu} \\ 0 & 0 \end{bmatrix} \end{align}\]

What is a next generation matrix?

Source: quantpie’s video.

A population consists of two groups: young and old.

• A young person on average infects 3 young and 2 old: \(\begin{bmatrix} 3 \\ 2 \end{bmatrix}\).
• An old person on average infects 1 young and 2 old: \(\begin{bmatrix} 1 \\ 2 \end{bmatrix}\).

Each group becomes a column in the next generation matrix (NGM):

\[\text{NGM} = \begin{bmatrix} 3 & 1 \\ 2 & 2 \end{bmatrix}\]

\(R_0\) is the root of equation:

\[\begin{align} \begin{bmatrix} 3 - \lambda & 1 \\ 2 & 2 - \lambda \end{bmatrix} & = 0 \\ \Leftrightarrow (3 - \lambda) \times (2 - \lambda) - 2 \times 1 & = 0 \\ \Leftrightarrow \lambda^2 - 5 \lambda + 6 - 2 & = 0 \\ \Leftrightarrow \lambda^2 - 5 \lambda + 4 & = 0 \end{align}\]

There are two roots \(\lambda = 4\) and \(\lambda = 1\), for an outbreak to occur \(R_0 > 1\), so here \(R_0 = 4\).

Step 5. Compute \(R_0\)

\(R_0\) is the eigenvalues of the NGM.

\[\begin{align} det(K - \lambda) & = \begin{bmatrix} \frac{\beta S \sigma}{(\sigma + \mu)(\gamma + \mu)} - \lambda & \frac{\beta S}{\gamma + \mu} \\ 0 & 0 - \lambda \end{bmatrix} \\ & = [\frac{\beta S \sigma}{(\sigma + \mu)(\gamma + \mu)} - \lambda][0 - \lambda] \end{align}\]

\[R_0 = \frac{\beta S \sigma}{(\sigma + \mu)(\gamma + \mu)}\]

Use NGM to compute \(R_0\) for SIR model

Consider a simple closed population SIR model.

\[\begin{align} \frac{dS}{dt} & = -\beta SI \\ \frac{dI}{dt} & = \beta SI - \gamma I\\ \frac{dR}{dt} & = \gamma I \end{align}\]

Step 1. Identify the infected compartments

For our SIR model, the infected compartment is \(I\).

Step 2. Write the NGM functions

\[\mathcal{F} = \beta SI\]

\[\mathcal{V} = \gamma I\]

Such that we have:

\[\frac{dI}{dt} = \mathcal{F} - \mathcal{V} = \beta SI - \gamma I\]

Step 3. Find the Jacobian matrix

\[F = \frac{\partial \mathcal{F}}{\partial I} = \frac{\partial [\beta SI]}{\partial I} = \beta S\]

\[V = \frac{\partial \mathcal{V}}{\partial I} = \frac{\partial [\gamma I]}{\partial I} = \gamma\]

Step 4 and 5. Compute the NGM and \(R_0\)

\[V^{-1} = \gamma^{-1} = \frac{1}{\gamma}\]

\[K = FV^{-1} = \frac{\beta S}{\gamma}\]

Here we also have \(R_0\).

\[R_0 = \frac{\beta S}{\gamma}\]

10.3 Epidemic final size

If there were no interventions or changes in behavior, the proportion of the population infected during the entire course of an epidemic would be approximately the non-zero solution of the equation:

$$$$

Bradshaw, W. J., Alley, E. C., Huggins, J. H., Lloyd, A. L., & Esvelt, K. M. (2021). Bidirectional contact tracing could dramatically improve COVID-19 control. Nature Communications, 12(1), 232. https://doi.org/10.1038/s41467-020-20325-7

Breban, R., Vardavas, R., & Blower, S. (2007). Theory versus Data: How to Calculate R0? PLOS ONE, 2(3), e282. https://doi.org/10.1371/journal.pone.0000282

Diekmann, O., Heesterbeek, J. A. P., & Metz, J. A. J. (1990). On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology, 28(4), 365–382. https://doi.org/10.1007/BF00178324

Driessche, P. van den. (2017). Reproduction numbers of infectious disease models. Infectious Disease Modelling, 2(3), 288–303. https://doi.org/10.1016/j.idm.2017.06.002

Driessche, P. van den, & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180(1), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6

Pandit, J. J. (2020). Managing the R0 of COVID-19: mathematics fights back. Anaesthesia, 75(12), 1643–1647. https://doi.org/10.1111/anae.15151