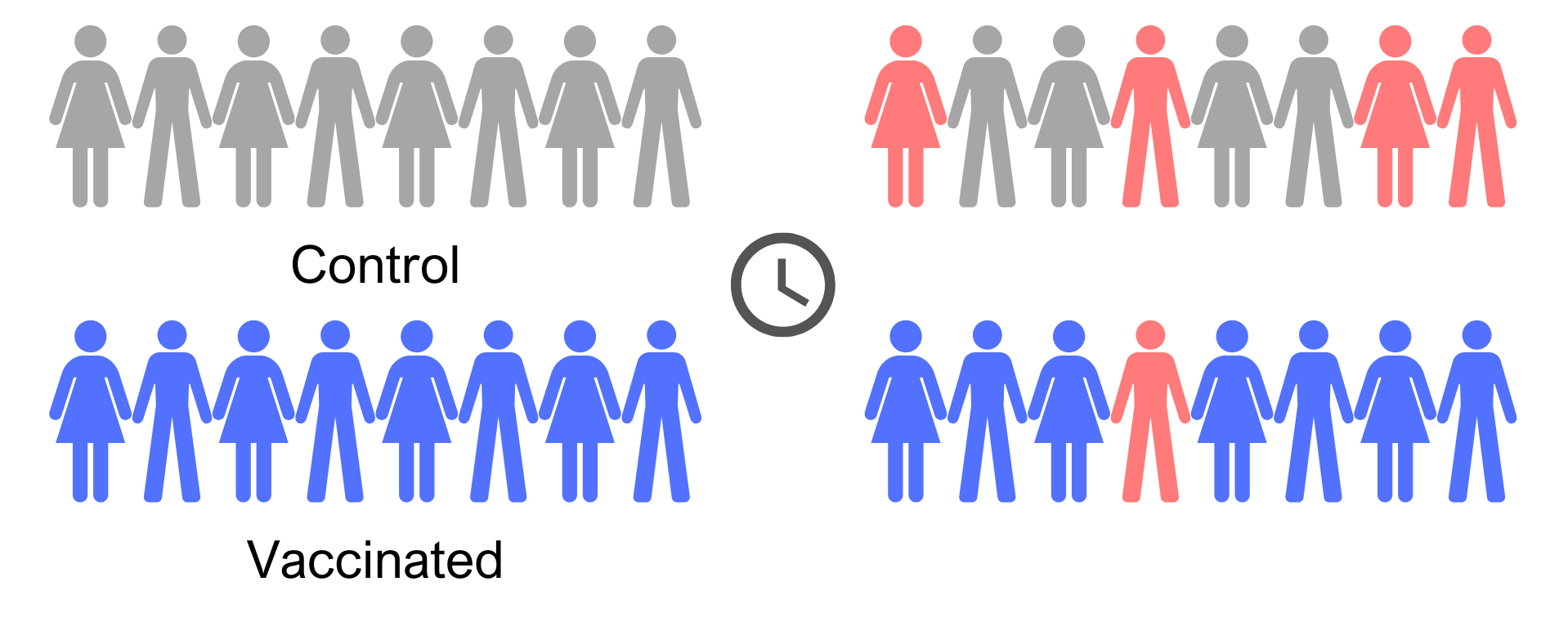
Shim, E., & Galvani, A. P. (2012). Distinguishing vaccine efficacy and effectiveness.
Vaccine,
30(47), 6700–6705.
https://doi.org/10.1016/j.vaccine.2012.08.045
Verani, J. R., Baqui, A. H., Broome, C. V., Cherian, T., Cohen, C., Farrar, J. L., Feikin, D. R., Groome, M. J., Hajjeh, R. A., Johnson, H. L., Madhi, S. A., Mulholland, K., O’Brien, K. L., Parashar, U. D., Patel, M. M., Rodrigues, L. C., Santosham, M., Scott, J. A., Smith, P. G., … Zell, E. R. (2017). Case-control vaccine effectiveness studies: Preparation, design, and enrollment of cases and controls.
Vaccine,
35(25), 3295–3302.
https://doi.org/10.1016/j.vaccine.2017.04.037